(16分)如图1所示,匀强磁场的磁感应强度B为0.5T.其方向垂直于倾角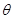 为30°的斜面向上。绝缘斜面上固定有
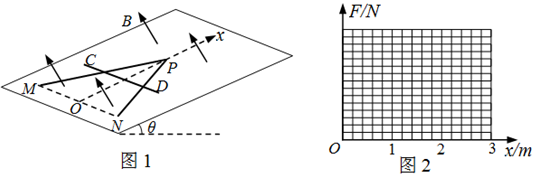
为30°的斜面向上。绝缘斜面上固定有 形状的光滑金属导轨MPN(电阻忽略不计),MP和NP长度均为2.5m,MN连线水平,长为3m。以MN中点O为原点、OP为x轴建立一维坐标系Ox。一根粗细均匀的金属杆CD,长度d为3m、质量m为1kg、电阻R为0.3Ω,在拉力F的作用下,从MN处以恒定的速度v=1m/s,在导轨上沿x轴正向运动(金属杆与导轨接触良好)。g取10m/s2。
形状的光滑金属导轨MPN(电阻忽略不计),MP和NP长度均为2.5m,MN连线水平,长为3m。以MN中点O为原点、OP为x轴建立一维坐标系Ox。一根粗细均匀的金属杆CD,长度d为3m、质量m为1kg、电阻R为0.3Ω,在拉力F的作用下,从MN处以恒定的速度v=1m/s,在导轨上沿x轴正向运动(金属杆与导轨接触良好)。g取10m/s2。
(1)求金属杆CD运动过程中产生产生的感应电动势E及运动到 处电势差
处电势差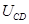 ;
;
(2)推导金属杆CD从MN处运动到P点过程中拉力F与位置坐标x的关系式,并在图2中画出F-x关系图象;
(3)求金属杆CD从MN处运动到P点的全过程产生的焦耳热。
(1)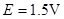 ,
,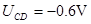 ;(2)
;(2) (0≤x≤2);(3)
(0≤x≤2);(3)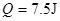
题目分析:
(1)金属杆CD在匀速运动过程中产生的感应电动势
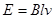 (l=d)
(l=d)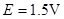 (D点电势高)
(D点电势高)
当x=0.8m时,金属杆在导轨间的电势差为零,设此时杆在导轨外的长度为l外则

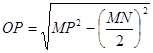 得
得 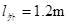
由楞次定律判断D点电势高,故CD两端电势差
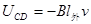
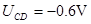
(2)杆在导轨间的长度l与位置x关系是 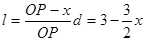
对应的电阻Rl为  电流
电流 
杆受的安培力F安 为
为 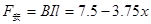
根据平衡条件得 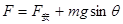
 (0≤x≤2)
(0≤x≤2)
画出的F-x图象如图所示。
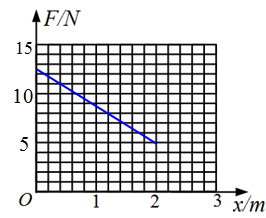
(3)外力F所做的功WF等于F-x图线下所围的面积,即
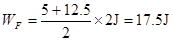
而杆的重力势能增加量 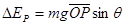
故全过程产生的焦耳热