问题
问答题
应用通项求导或逐项积分，求下列幂级数的和函数．
(1)
；
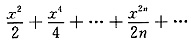(2)x2+2x3+3x4+…+nxn+1+…．
答案
参考答案：[考点点击] 本题考查幂级数的和函数．
[要点透析] (1)设
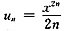，故
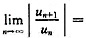x2。则当|x2|＜1时原级数收敛，故原级数的收敛半径为R=1，当x=±1时，则原级数可化为
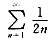，故其发散·故原级数的收敛域为(-1，1)
设
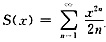，在x∈(-1，1)内逐项求导得
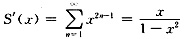
故
x2)，x∈(-1，1)．
(2)设an=n，
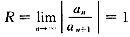，当x=±1时
原级数均发散，故原级数的收敛域为(-1，1)
设
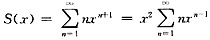，设f(x)=I
，逐项积分得
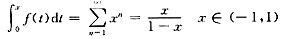
故
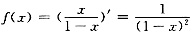
故和函数
