在△ABC中,角A、B、C的对应边分别为a、b、c,已知复数z1=3+2sinA•i,z2=sinA+(1+cosA)i(i是虚数单位),它们对应的向量依次为
(1)求∠A的值; (2)求cos(C-
|
解(1)由已知,
=(3,2sinA),OZ1
=(sinA,1+cosA),(2分)OZ2
∵
∥OZ1
,∴3(1+cosA)-2sin2A=0.OZ2
2cos2A+3cosA+1=0,(4分)
cosA=-1(舍去)或cosA=-
.1 2
∵A∈(0,π),A=
.(6分)2π 3
(2)∵
(c-b)=a,7
∴由正弦定理,得
(sinC-sinB)=sinA=7
,(9分)3 2
sinC-sin(
-C)=π 3
,21 14
sin(C-3
)=π 6
,sin(C-21 14
)=π 6
,(12分)7 14
∵0<C-
<π 6
,∴cos(C-π 2
)=π 6
=1- 1 28
=27 28
.(14分)3 21 14

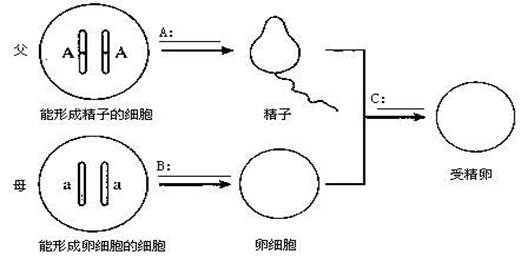
 ”代表 ,A和a代表 。
”代表 ,A和a代表 。