阅读下列说明,回答问题1至问题3,将解答填入对应栏内。
【说明】
快速排序是一种典型的分治算法。采用快速排序对数组A[p..r]排序的3个步骤如下。
1.分解:选择一个枢轴(pivot)元素划分数组。将数组A[p..r]划分为两个子数组 (可能为空)A[p..q-1]和A[q+1..r],使得A[q]大于等于A[p..q-1)中的每个元素,小于 A[q+1..r]中的每个元素。q的值在划分过程中计算。
2.递归求解:通过递归的调用快速排序,对子数组A[p..q-1]和A[q+1..r]分别排序。
3.合并:快速排序在原地排序,故不需合并操作。
| 【问题3】 (1)待排序数组是否能被较均匀地划分对快速排序的性能有重要影响,因此枢轴元素的选取非常重要。有人提出从待排序的数组元素中随机地取出一个元素作为枢轴元素,下面是随机化快速排序划分的伪代码——利用原有的快速排序的划分操作,请填充其中的空缺处。其中,RANDOM(i,j)表示随机取i到j之间的一个数,包括i和j。 RANDOMIZED- PARTITION(A,p,r){ i=RANDOM(p,rl); 交换 (8) 和 (9) ;//注:空(8)和空(9)答案可互换,但两空全部答对方可得分 return PARTITION (A,p,r); } (2)随机化快速排序是否能够消除最坏情况的发生 (10) 。(是或否) |
参考答案:
解析:A[i] (9)A[r] (10)否
注;空(8)和空(9)答案可以互换
试题四
[分析]:
本题考查算法的设计与分析技术。
问题1考查快速排序算法的伪代码,快速排序最核心的处理是进行划分,即 PARTITION操作,根据枢轴元素的值,把一个较大的数组分成两个较小的子数组,一个子数组的所有元素的值小于等于枢轴元素的值,一个子数组的所有元素的值大于枢轴元素的值,而子数组内的元素不排序。划分时,以最后一个元素为枢轴元素,从左到右依次访问数组的每一个元素,判断其与枢轴元素的大小关系,并进行元素的交换,如图4-1所示:
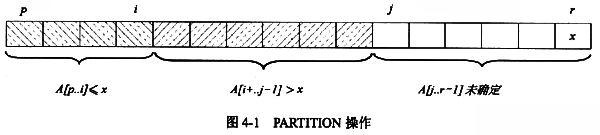
在问题1给出的伪代码中,当循环结束后,A[p..i]中的值应小于等于枢轴元素值x,而A[i+1..r-1]中的值应大于枢轴元素值x。此时A[i+1)是第一个比A[r]大的元素,因此 A闭与A[i+1]交换,得到划分后的两个子数组。PARTITION操作返回枢轴元素的位置,因此返回值为i+1。
问题2考查的是快速排序算法的时间复杂度分析。当每次能作均匀划分时,算法为最佳情况,此时时间复杂度可以通过计算递归式T(n)=2T(n/2)+O(n),得到时间复杂度为O(nlgn):当每次为极端不均匀划分时,即长度为n的数组划分后一个子数组为n-1,一个为0,算法为最坏情况,此时时间复杂度可以通过计算递归式T(n)=T(n-1)+O(n),得到时间复杂度为O(n2);平均情况的分析较为复杂,我们可以假设数组每次划分为 9/10:1/10,此时时间复杂度可以通过计算递归式T(n)=T(9/10)+T(1/10)+O(n),得到时间复杂度为O(nlgn),因此在平均情况下快速排序仍然有较好的性能,时间复杂度为 O(nlgn)。当所有的n个元素具有相同的值时,可以认为数组已经有序,此时每次都划分为长度为n-1和0的两个子数组,属于最坏情况。
问题3中,由于随机化的快速排序的划分调用了传统的快速排序算法的PARTITION操作,而传统的划分每次以数组的最后一个元素作为枢轴元素,因此,随机化的划分操作中每次先随机获得一个元素,将其与最后一个元素交换。随机化的快速排序消除了输入数据的不同排列对算法性能的影响,降低了极端不均匀划分的概率,但不能保证不会导致最坏情况的发生。
