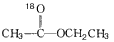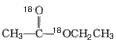参考答案：C

解析：

[分析]： 企业库存管理问题就是这方面的应用。在企业原材料年需量确定，希望平均分多次订货的情况下，订货费用与订货次数成正比，库存管理费用则与订货次数成反比。为使总费用最低，就要求正比函数与反比函数之和的极小值。

函数f(x)=4x+9/x中，x的范围规定为x＞0。当x非常小时，或x非常大时，f(x)都会非常大，但f(x)总是大于0，因此，从趋势看，f(x)没有极大值，应该有极小值。

f(x)的导函数f(x)=4-9/x²。当4=9/x²时，导函数值为0。也就是说，当4x=9/x(或 x=3/2)时，f(x)会有极值。当x＜3/2时，f(x)＜0，f(x)是递减的；当x＞3/2时，f(x)＞0，f(x)是递增的，因此，在4x=9/x(或x=3/2)时，f(x)有极小值。

在库存管理问题中，只有当订货费用(正比函数)与库存管理费用(反比函数)相等时，总费用才能达到极小值。