问题
填空题
设A为三阶矩阵,其特征值为λ1=-2,λ2=λ3=1,其对应的线性无关的特征向量为α1,α2,α3,令P=(4α1,α2-α3,α2+2α3),则p-1(A*+3E)P为______.
答案
参考答案:
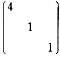
解析:[详解] 因为A的特征值为λ1=-2,λ2=λ3=1,所以A*的特征值为μ1=1,μ2=μ3=-2,A*+3E的特征值为4,1,1,又因为4α1,α2-α3,α2+2α3也为A的线性无关的特征向量,所以4α1,α2-α3,α2+2α3也是A*+3E的线性无关的特征向量,所以
[*]

