问题
解答题
已知sinα，sinβ是方程8x2-6kx+2k+1=0的两个根，且α、β的终边互相垂直，求k的值。
答案
解：∵α，β的终边互相垂直，不妨设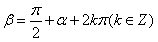
，
∴sinβ=sin(α+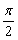
+2kπ)=cosα，
那么sinα，cosα是方程8x2-6kx+2k+1=0的两个根，
所以k应满足：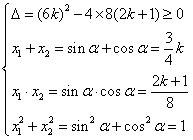
，
消去sinα，cosα，得9k2-16k-8≥0且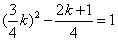
，
∴
。
搜题请搜索小程序“爱下问搜题”
已知sinα，sinβ是方程8x2-6kx+2k+1=0的两个根，且α、β的终边互相垂直，求k的值。
解：∵α，β的终边互相垂直，不妨设，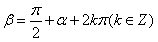
∴sinβ=sin(α+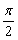+2kπ)=cosα，
那么sinα，cosα是方程8x2-6kx+2k+1=0的两个根，
所以k应满足：，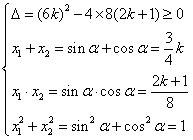
消去sinα，cosα，得9k2-16k-8≥0且，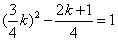
∴。