问题
问答题
设f(x)为[-a，a]上的连续的偶函数且f(x)＞0，令
.
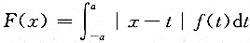(Ⅰ)证明：F’(x)单调增加．
(Ⅱ)当x取何值时，F(x)取最小值
(Ⅲ)当F(x)的最小值为f(a)-a2-1时，求函数f(x)．
答案
参考答案：[*]
[*]
因为F"(x)=2f(x)＞0，所以F’(x)为单调增加的函数．
(Ⅱ)因为[*]为偶函数，所以F’(0)=0，又因为F"(0)＞0，所以x=0为F’(x)的唯一极小点，也为最小点．
故最小值为[*]．
(Ⅲ)由[*]=f(a)-a2-1两边求导得
2af(a)=f’(a)-2a
于是f’(x)-2xf(x)=2x，
解得 [*]，
在 [*]中令a=0得f(0)=1，则C=2，于是f(x)=[*]-1．