问题
问答题
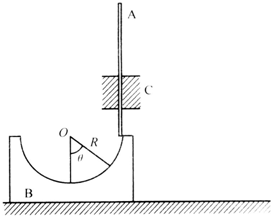
如图所示,B是质量为mB、半径为R的光滑半球形碗,放在光滑的水平桌面上.A是质为mA的细长直杆,被固定的光滑套管C约束在竖直方向,A可自由上下运动.碗和杆的质量关系为:mB=2mA.初始时,A杆被握住,使其下端正好与碗的半球面的上边缘接触(如图).然后从静止开始释放A,A、B便开始运动.设A杆的位置用θ 表示,θ 为碗面的球心O至A杆下端与球面接触点的连线方向和竖直方向之间的夹角.求A与B速度的大小(表示成θ 的函数).
答案
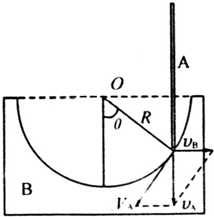
由题设条件知,若从地面参考系观测,则任何时刻,A沿竖直方向运动,设其速度为vA,B沿水平方向运动,设其速度为vB,若以B为参考系,从B观测,则A杆保持在竖直方向,它与碗的接触点在碗面内作半径为R的圆周运动,速度的方向与圆周相切,设其速度为VA.杆相对地面的速度是杆相对碗的速度与碗相对地面的速度的合速度,速度合成的矢量图如图中的平行四边形所示.由图得VAsinθ=vA (1)
VAcosθ=vB (2)
因而,vB=vAcotθ (3)
选AB组成的系统为研究对象,由能量守恒:
mAgRcosθ=
mA1 2
+v 2A
mB1 2
(4)v 2B
由(3)、(4)两式及mB=2mA得
vA=sinθ
(5)2gRcosθ 1+(cosθ)2
vB=cosθ
(6)2gRcosθ 1+(cosθ)2
答:两物体速度为:vA=sinθ2gRcosθ 1+(cosθ)2
vB=cosθ2gRcosθ 1+(cosθ)2
