问题
问答题
已知向量组(Ⅰ)α1，α2，α3；(Ⅱ)α1，α2，α3，α4；(Ⅲ)α1，α2，α3，α5，如果各向量组的秩分别为r(Ⅰ)=r(Ⅱ)=3，r(Ⅲ)=4．
证明：向量组α1，α2，α3，α5-α4的秩为4．
答案
参考答案：因r(Ⅰ)=r(Ⅱ)=3，所以α1，α2，α3线性无关，而α1，α2，α3，α4线性相关．故存在实数λ1，λ2，λ3使
α1=λ1α1+λ2α2+λ3α3 ①
设有数是k1，k2，k3，k4，使得
k1α1+k2α2+k3α3+k4(α5-α4)=0， ②
将①代入②，化简得
(k1-λ1k1)α1+(k2-λ2k4)α2+(k3-λ3k4)α3+k4α5=0，
由，r(Ⅲ)=4知α1，α2，α3，α5线性无关，
所以
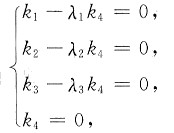
得k1=k2=k3=k4=0．
故α1，α2，α3，α5-α4线性无关，其秩为4．
解析：[考点提示] 向量组的秩．