设A,B是二随机事件;随机变量
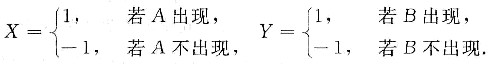
试证明随机变量X和Y不相关的充分必要条件是A与B相互独立.
参考答案:由题设,记P(A)=p1,则P(X-1)=p1,从而P(X=-1)=1-p1,记P(B)=p2,则P(Y=1)=p2,且P(Y=-1)=1-p2.因此有
E(X)=p1-(1-p1)=2p1-1,E(Y)=p2-(1-p2)=2p2-1.
由于X,Y的取值只能为1和-1,从而
P(XY=1)=P(X-1,Y=1)+P(X=-1,Y=-1)
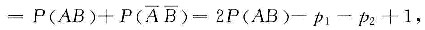
P(XY=-1)=1-[2P(AB)-P1-p2+1]
=1-2P(AB)+p1+p2-1=p1+p2-2P(AB),
所以E(XY)=2P(AB)-p1-p2+1-[p1+p2-2P(AB)]
=2P(AB)-p1-p2+1-p1-p2+2P(AB)
=4P(AB)-2p1-2p2+1,
因此cov(X,Y)=E(XY)-E(X)·E(Y)
=4P(AB)-2p1-2p2-1-(2p1-1)(2p2-1)
=4P(AB)-2p1-2p2+1-4p1p2+2p1+2p2-1
=4P(AB)-4p1p2=4[P(AB)-P(A)P(B)],
显然cov(XY)=0
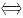 P(AB)=P(A)P(B),即X与Y不相关的充要条件是A与B相互独立.
P(AB)=P(A)P(B),即X与Y不相关的充要条件是A与B相互独立.
解析:[考点提示] 独立性、相关性.
