问题
问答题
设
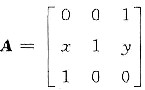 有三个线性无关的特征向量,求x和y应满足的条件.
有三个线性无关的特征向量,求x和y应满足的条件.
答案
参考答案:特征方程为
|λE-A|=λ3-λ2-λ+1=(λ-1)2(λ+1)=0,
即特征值λ1=1(二重),λ2=-1.
欲使λ1=1有两个线性无关的特征向量,矩阵

的秩必须等于1,故
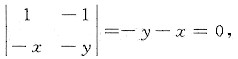
于是得x+y=0.
因为不同特征值所对应的特征向量线性无关,所以矩阵A要有三个线性无关的特征向量,必须满足条件x+y=0.
解析:[考点提示] 本题应先求出特征值,由题设3阶矩阵要有三个线性无关的特征向量,重特征值对应的线性无关特征向量的个数必须等于特征值的重数,相应的特征矩阵的秩r(λE-A)=n-特征值的重数,由此导出参数应满足的条件.
[评注] 下面三个命题互为充要条件:
1.n阶矩阵A可对角化;
2.A有n个线性无关的特征向量;
3.A的任何重特征值对应的线性无关的特征向量个数等于其重数.
