问题
问答题
设线性方程组
(1) 证明：若α1，α2，α3，α4两两不相等，则此线性方程组无解；
(2) 设α1=α3=k，α2=α4=-k(k≠0)，且已知β1、β2是该方程组的两个解，其中
写出此方程组的通解．
答案
参考答案：(1) 增广矩阵
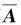的行列式
由a1，a2，a3，a4两两不相等，知
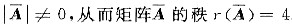．但系数矩阵A的秩r(A)≤3，故r(A)≠r(A)，因此方程组无解．
(2) 当a1=a3=k，a2=a4=-k(k≠0)时，方程组为
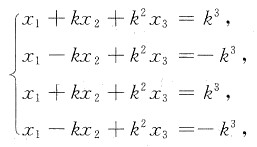
即
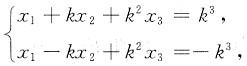
因为
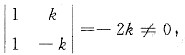
故
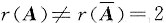，从而方程组有解，且对应的导出方程组的基础解系应含有3-2=1个解向量．因为β1，β2是原齐次方程组的两个解，故
是对应齐次线性方程组的解，且ξ≠0，故ξ是导出方程组的基础解系．
于是原齐次线性方程组的通解为
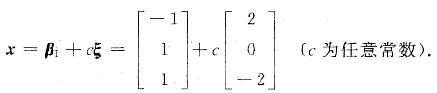
解析：[考点提示] 要证明线性方程组无解，只需证明系数矩阵A的秩不等于增广矩阵[*]的秩，证明中注意利用范德蒙行列式的性质以及矩阵的秩小于或等于行数和列数的性质．