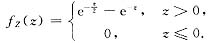问题
问答题
已知随机变量X的概率密度为
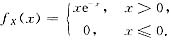在X=(x＞0)的条件下，随机变量Y在区间(0，x)上服从均匀分布，求：
(Ⅰ)随机变量X与Y的联合概率密度f(x，y)，X与Y是否独立，为什么
(Ⅱ)计算条件概率
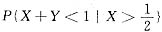与
；
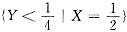(Ⅲ)求证：Z=X-Y服从参数λ=1的指数分布．
答案
参考答案：由题设知：在X=x(x＞0)的条件下，Y的条件密度为
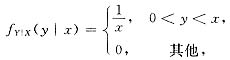
根据乘法公式得
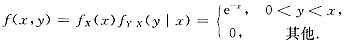
由于
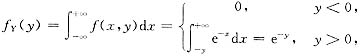
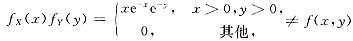，故X与Y不独立．
(Ⅱ)
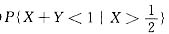
其中
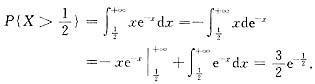
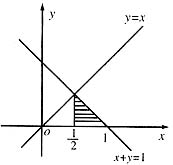
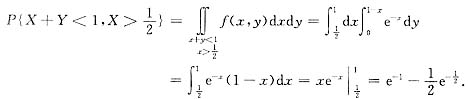
所以
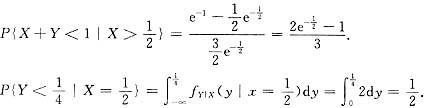
(Ⅲ)通过计算Z=X-Y的分布给出证明．其方去有：
方法一(分布函数法)Z=X-Y分布函数
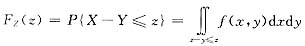
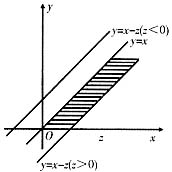
当z≤0时，Fz(z)=0，
当z＞0时，
综上得
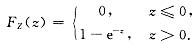
由此可知Z=X-Y服从参数λ=1的指数分布．
方法二(公式法)已知(X，Y)～f(x，y)，则Z=X-Y的概率密度fz(z)=
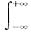f(x+y+z).其中
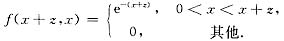
由此可知：当z≤0时，fz(z)=0；
当z＞0时，
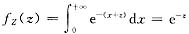，综上得
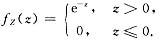
所以Z=X-Y服从参数λ=1的指数分布．
[注] 仿照上述方法可以求得Z—X+Y的概率密度fz(z)．
方法一(分布函数法)
Z=X+Y的分布函数
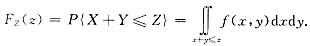
由f(x，y)非零定义域知：当z≤0时，Fz(x)=0；当z＞0时，
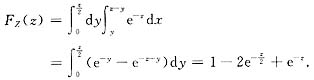
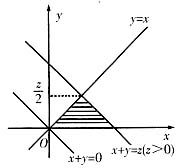
综上得
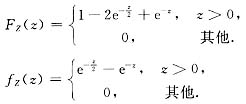
方法二(公式法)已知(X，Y)～f(x，y)，则Z=X+Y的概率密度fz(z)=
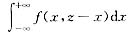其中
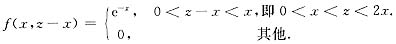
由此可知：当z≤0时，fz(z)=0；
当z＞0时，
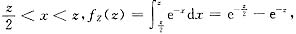
综上得
