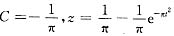问题
问答题
设f(x)为[0，+∞)上的正值连续函数，已知曲线．
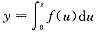和两坐标轴及直线x=t(t＞0)所围区域绕y轴旋转所得体积与曲线y=f(x)和两坐标轴及直线x=t(t＞0)所围区域的面积之和为t2，求曲线y=f(x)的方程．
答案
参考答案：[解] 曲线
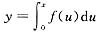和两坐标轴及直线x=t(t＞0)所围区域绕y轴旋转所得体积为
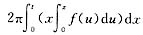
曲线y=f(x)和两坐标轴及直线x=t(t＞0)所围区域的面积为
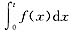
则
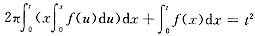上式两端对t求导得
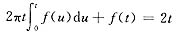
令
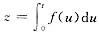，则
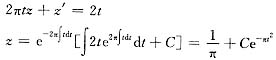
由z(0)=0知，
