问题
单项选择题
设g(x)可导，且x→0时，g(x)是x的高阶无穷小，则当x→0时，必有
(A) g′(x)是无穷小量．
(B)
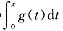是x2的高阶无穷小．
(C)
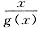是无穷大量．
(D) 若G′(x)=g(x)，则G(x)是x高阶无穷小．
答案
参考答案：B
解析： 由于
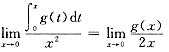(洛必达法则)=0
则
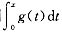是x2的高阶无穷小，故应选(B)．
[评注] 本题的其余选项都不正确．事实上，若取
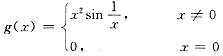
容易验证g(x)可导，且当x→0时，g(x)是x的高阶无穷小，但
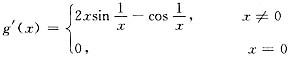
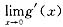不存在，由于
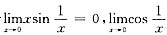不存在，则(A)不正确．若取g(x)=0，显然g(x)符合题设条件，但
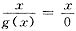无意义，则(C)不正确．若取g(x)=x2，
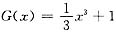，显然当x→0时，g(x)是x的高阶无穷小，且G′(x)=g(x)，但
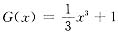不是x的高阶无穷小，则(D)不正确．