问题
问答题
证明：当x＞0时，有不等式(1+x)ln(1+x)＞arctanx．
答案
参考答案：[证] 作辅助函数f(x)=(1+x)ln(1+x)-arctanx．
显然，f(x)在x≥0时连续，且f(0)=0，又
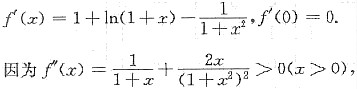
故f(x)在x＞0时严格单调递增，所以当x＞0时，有f(x)＞f(0)=0，即有
(1+x)ln(1+x)＞arctanx．
搜题请搜索小程序“爱下问搜题”
证明：当x＞0时，有不等式(1+x)ln(1+x)＞arctanx．
参考答案：[证] 作辅助函数f(x)=(1+x)ln(1+x)-arctanx．
显然，f(x)在x≥0时连续，且f(0)=0，又
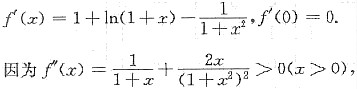
故f(x)在x＞0时严格单调递增，所以当x＞0时，有f(x)＞f(0)=0，即有
(1+x)ln(1+x)＞arctanx．