问题
问答题
设α1，α2，α3，α4，β为四维列向量，A=[α1，α2，α3，α4]，已知Ax=β的通解为
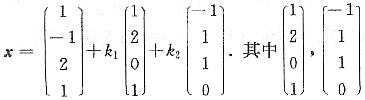为对应齐次方程组的基础解系，k1，k2为任意常数．令B=[α1，α2，α3]，试求By=β的通解．
答案
参考答案：
解析： 由题设知：r(A)=2，且有β=α1-α2+2α3+α4，
于是有α3=α1-α2，α4=-α1-2α2，β=2α1-5α2+0α3．可见α1，α2线性无关，秩r(B)=2，且
为By=β的特解，又由α1-α2-α3=0知
为By=0的非零解，可作为基础解系，故By=β的通解为
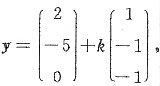其中k为任意常数．