问题
问答题
设n阶实对称矩阵A的n个特征值λi(i=1，2，…，n)互异，X1为λ1对应的单位特征向量，证明：方阵A-λ1X1
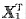的特征值为0，λ2，…，λn．
答案
参考答案：[证] 设Xi为λi(i=1，2，…，n)对应的单位特征向量，则当i≠j时，
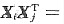0．于是
当
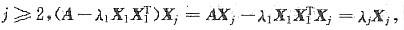
又
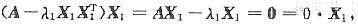
所以方阵
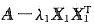的特征值为0，λ2，…，λn．
搜题请搜索小程序“爱下问搜题”
设n阶实对称矩阵A的n个特征值λi(i=1，2，…，n)互异，X1为λ1对应的单位特征向量，证明：方阵A-λ1X1
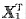的特征值为0，λ2，…，λn．
参考答案：[证] 设Xi为λi(i=1，2，…，n)对应的单位特征向量，则当i≠j时，
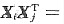0．于是
当
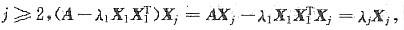
又
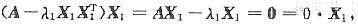
所以方阵
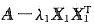的特征值为0，λ2，…，λn．