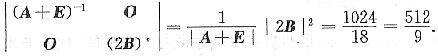问题
填空题
设A,B为三阶相似矩阵,A的两个特征值为1,2,行列式|B|=4,则
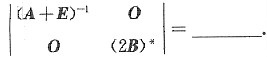
答案
参考答案:
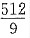
解析:
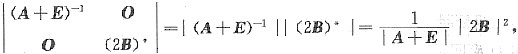
因为A的两个特征值为1,2,A,B相似且|B|=4可知|A|=4,设A的另一特征值为λ,则有|A|=λ×1×2=4
 λ=2,所以A的特征值为1,2,2,于是
λ=2,所以A的特征值为1,2,2,于是
A+E的特征值为2,3,3,所以|A+E|=2×3 X 3=18,
且|2B|2=64|B|2=1024,
所以
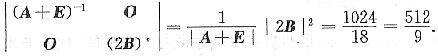
设A,B为三阶相似矩阵,A的两个特征值为1,2,行列式|B|=4,则
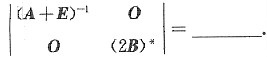
参考答案:
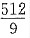
解析:
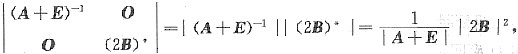
因为A的两个特征值为1,2,A,B相似且|B|=4可知|A|=4,设A的另一特征值为λ,则有|A|=λ×1×2=4
 λ=2,所以A的特征值为1,2,2,于是
λ=2,所以A的特征值为1,2,2,于是
A+E的特征值为2,3,3,所以|A+E|=2×3 X 3=18,
且|2B|2=64|B|2=1024,
所以