问题
单项选择题
设f(x)在[a，b]上可导，又f’(x)+[f(x)]2-
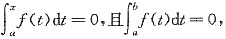则
在(a，b)内______
A．恒为负．
B．恒为零．
(c)恒为正．
D．符号不确定．
答案
参考答案：B
解析： F(x)=
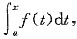则F(a)=F(b)=0．
变为F’’(x)+[F’(x)]2-F(x)=0．(*)
若
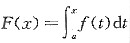在(a，b)内不恒为零，则F(x)在(a，b)内可以取到正的最大值(此时也为极大值)或负的最小值(此时也为极小值)，不妨设
则F’(x1)=0，代入(*)式可得
f’’(x1)=-[F’(x1)]2+F(x1)＞0，由极值的判定条件可知，F(x)在x=x1处取到极小值，矛盾．
同理可证，若F(x2)=
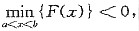同样得到矛盾．
故F(x)≡0，即选B．