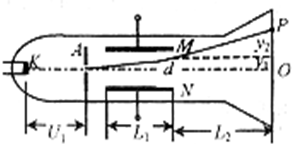
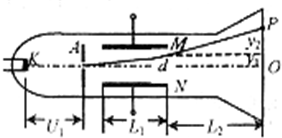
如图所示为真空示波管的示意图,电子从灯丝K发出(初速度不计),经灯丝与A板间的加速电压U1加速,从A板中心孔沿中心线KO射出,然后进入由两块平行金属板M、N形成的偏转电场中(偏转电场可视为匀强电场),电子进入偏转电场时的速度与电场方向垂直,电子经过偏转电场偏转打在荧光屏上的P点,已知M、N两板间的电压为U2,两板间的距离为d,板长为L1,板右端到荧光屏的距离为L2,电子的质量为m,电荷量为e.求:
(1)电子穿过A板时的速度大小;
(2)电子从偏转电场射出时的侧移量y1;
(3)荧光屏上P点到中心位置O点的距离.
(1)设电子经电压U1加速后的速度为V0,
由动能定理得:eU1=
mv02,解得:v0=1 2
;2eU1 m
(2)电子以速度υ0进入偏转电场后,垂直于电场方向做匀速直线运动,
沿电场方向做初速度为零的匀加速直线运动,设偏转电场的电场强度为E,
电子在偏转电场中运动的时间为t1,电子的加速度为α,离开偏转电场时的侧移量为y1,
由牛顿第二定律得:F=eE2=e
=ma,解得:a=U2 d
,eU2 md
由运动学公式得:L1=v0t1,y1=
at12,解得:y1=1 2
;U2 L 21 4U1d
(3)设电子离开偏转电场时沿电场方向的速度为υy,
由匀变速运动的速度公式可知υy=at1;
电子离开偏转电场后做匀速直线运动,
设电子离开偏转电场后打在荧光屏上所用的时间为t2,
电子打到荧光屏上的侧移量为y2,如图所示,
水平方向:L2=v0t2,竖直方向:y2=vyt2,解得:y2=
;U2L1L2 2dU1
P至O点的距离y=y1+y2=
;(2L2+L1)U2L1 4U1d
答:(1)电子穿过A板时的速度大小为
;2eU1 m
(2)电子从偏转电场射出时的侧移量为
;U2 L 21 4U1d
(3)荧光屏上P点到中心位置O点的距离为
.(2L2+L1)U2L1 4U1d
