如图6-4-11所示,A、B是静止在水平地面上完全相同的两块长木板.A的左端和B的右端相接触.两板的质量皆为M="2.0" kg,长度皆为l="1.0" m.C是一质量为m="1.0" kg的小物块,现给它一初速度v0="2.0" m/s,使它从B板的左端开始向右滑动.已知地面是光滑的,而C与A、B之间的动摩擦因数皆为μ=0.10.求最后A、B、C各以多大的速度做匀速运动.取重力加速度g="10" m/s2.

图6-4-11
0.563 m/s 0.155 m/s 0.563 m/s
先假设小物块C在木板B上移动x距离后,停在B上,这时A、B、C三者的速度相等,设为v.由动量守恒得
mv0=(m+2M)v ①
在此过程中,木板B的位移为s,小木块C的位移为s+x.由功能关系得
-μmg(s+x)=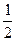 mv2-
mv2-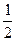 mv02
mv02
μmgs=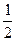 ·2Mv2
·2Mv2
相加得-μmgx=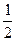 (m+2M)v2-
(m+2M)v2-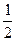 mv02 ②
mv02 ②
解①②两式得x=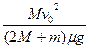
代入数值得x="1.6" m
x比B板的长度l大,这说明小物块C不会停在B板上,而要滑到A板上.设C刚滑到A板上的速度为v1,此时A、B板的速度为V1,则由动量守恒得mv0=mv1+2MV1
由功能关系得
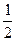 mv02-
mv02-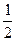 mv12-
mv12-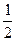 ·2MV12=μmgl
·2MV12=μmgl
以题给数据代入解得V1=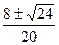 m/s
m/s
v1=2-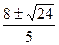 m/s=
m/s=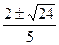 m/s
m/s
由于v1必是正数,故合理的解是
V1=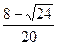 m/s="0.155" m/s v1=
m/s="0.155" m/s v1= m/s=1.38 m/s
m/s=1.38 m/s
当滑到A之后,B即以V1="0.155" m/s做匀速运动,而C以v1="1.38" m/s的初速在A上向右运动.设在A上移动了y距离后停止在A上,此时C和A的速度为v2,由动量守恒得
MV1+mv1=(m+M)v2
解得v2="0.563" m/s
由功能关系得
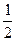 mv12+
mv12+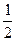 MV12-
MV12-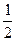 (m+M)v22=μmgy
(m+M)v22=μmgy
解得y="0.50" m
y比A板的长度小,故小物块C确实是停在A板上.最后A、B、C的速度分别为vA=v2="0.563" m/s,vB=v1="0.155" m/s,vC=vA="0.563" m/s.
