问题
问答题
设函数
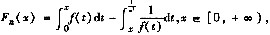其中n=1，2，3，…为任意自然数，f(x)为[0，+∞)上正值连续函数．求证：
(Ⅰ)Fn(x)在(0，+∞)存在唯一零点xn；
(Ⅱ)
收敛；
(Ⅲ)
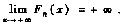
答案
参考答案：[分析与证明] (Ⅰ)Fn(x)在[0，+∞)内可导(也就必然连续)，又
[*]
[*]Fn(x)在[*]存在零点，记为xn则Fn(xn)=0．又
[*]
[*]有唯一零点，就是这个xn．
(Ⅱ)在前面的证明中已得估计式
[*]
因[*]收敛，由比较原理知，[*]收敛．又
ln(1+xn)～xn (n→+∞)
[*]收敛．
(Ⅲ)方法1° 前面已导出
[*]
方法2° 直接由
[*]
同样得[*]