问题
问答题
设f(x)在点x=0的某一邻域有二阶连续导数，且
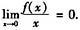
试证：级数
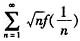绝对收敛。
答案
参考答案：[*]
由于正项级数[*]收敛，依正项级数比较判别法的极限形式知[*]收敛，即级数[*]绝对收敛。
解析：[考点] 证明数项级数绝对收敛
搜题请搜索小程序“爱下问搜题”
设f(x)在点x=0的某一邻域有二阶连续导数，且
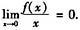
试证：级数
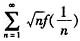绝对收敛。
参考答案：[*]
由于正项级数[*]收敛，依正项级数比较判别法的极限形式知[*]收敛，即级数[*]绝对收敛。
解析：[考点] 证明数项级数绝对收敛