如图所示的光滑水平面上，质量为M的平板车上依次放有5个质量均为m的小滑块(不计其大小)，质量关系为M＝5 m，已知平板车长L＝1 m，小滑块与平板车间的动摩擦因数μ＝9/20，g＝10 m/s2。现突然给最左端的小滑块沿平板向右的速度v0，当其相对地的速率降至v0/2时恰好与前方的第2个滑块相碰。碰撞时间极短，碰撞后两滑块的速度变为对方碰撞前的速度(也叫速度交换)。以后将陆续发生小滑块相碰，碰撞时间都很短，碰后均交换速度。最后第5个滑块恰好滑至平板车右端而与平板车相对静止。
(1)求v0的值；
(2)写出第一个小滑块运动中其相对地的最上速度的表达式；
(3)求平板车匀加速运动过程中的位移s。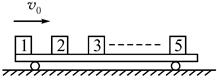
(1)3.14 m/s (2)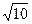
(3)0.1 m
第一个滑块以初速度v0在平板车上作匀减速运动。平板车在滑动摩擦力作用下带着上面的其他小物体一起向右做匀加速运动。第1个小滑块与第2个小滑块相碰后它立即取得与车相同的速度而随车一起做匀加速运动。第二个小滑块获得第1个小滑块的速度而做匀减速运动。以后依次为第2个小滑块与第3个小滑块相碰，各自交换速度，分别做匀加速运动与匀减速运动，直至第5个小滑块滑至平板车的最右端，这一过程中各个小滑块相对平板车滑动的距离之和等于平板车的长度，最后所有小滑块与车取得相同的速度。
根据动量守恒定律可以求得最后各滑块与车的共同速度v
mv0＝(M＋5m)v
根据能量转化关系有 μmg·L＝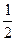
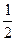mv02－（M＋5m）v2
由此解得 v0＝
代入数据 M＝5m,μ＝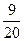
，L＝1 m，得v0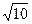＝ m/s＝3.14 m/s
(2) 第1个滑块与第2个滑块相碰后的速度即为它运动的最小速度，根据题意知这一速度就是碰撞前平板车的速度v1，由动量守恒定律得
mv0＝m·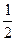v0＋(M＋5 m)v1
解得 v1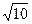＝v018
(3)加速度a＝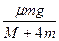
＝0.5 m/s2
加速过程结束后平板车的速度由前面可得v＝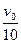
平板车的位移s＝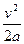
＝0.1 m