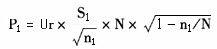X注册会计师对Y公司2004年末应收账款进行测试时,依据Y公司2004年12月31日应收账款明细账得知该公司共有2000家债务单位,账面余额合计为7760万元。X注册会计师拟运用抽样方法函证应收账款账面余额。设定的计划抽样误差为土5万元,可信赖程度为95%(相应的可信赖程度系数为1.96)。
要求:
(1)假定X注册会计师决定使用不重复抽样方法,估计的样本离差为S=0.014万元,请计算确定应收账款函证的样本量;
(2)假定按要求(1)中样本量及相应的样本值计算确定的样本标准离差S=0.016万元,请问X注册会计师是否需要增加累计样本量如需增加,增加到多少
(3)假定按照要求(2)中样本量估计的总体标准离差为0.015万元,请问X注册会计师是否需要增加累计样本量如需增加,增加到多少
(4)假定按(3)确定的样本量得到样本账面余额为566万元,审查后认定的余额为510万元,分别运用均值估计、比率估计及差额估计方法推断应收账款的总体余额及可信赖程度
为95%的估计区间。
(5)根据(4)中计算结果,指出X注册会计师确定最终估计的应收账款总体余额。列出计算过程,金额以万元为单位,保留小数点后4位。
参考答案:
(1)由命题条件知,总体规模为N=2 000,计划抽样误差为Pa=5,可信赖程度系数为 Ur=1.96,估计的总体标准离差为S=0.014,在重复抽样方式下,样本量为:
n’=(1.96×0.014× 2 000/5)2=120.47
在不重复抽样方式下,样本量为:
n=120.47×2 000/(120.47+2 000)=113.6≈114
(2)当S=0.016时,按公式(3),P1=5.34>Pa,需要增加样本量。将S=0.016代入公式(1)中,得n’=157.35,再按公式(2),n=145.87≈146,即需要增加32个样本数据。
(3)当S=0.015时,按公式(3),P1=4.6853<Pa,X注册会计师不再需要增加样本量。
(4)在均值估计方法下,推断的应收账款总体余额为510÷146× 2 000=6 986.3014万元,可信赖程度为95%的估计区间为[6 986.3014±4.6853] = [6 981.6161-6 990.9867];
在比率估计方法下,推断的应收账款总体余额为510÷566× 7 760=6 992.2261万元,可信赖程度为95%的估计区间为[6 992.2261±4.6853] = [6 987.5408~6 996.9114];
在差额估计方法下,样本平均差额为(510-566) ÷146=-0.3836,推断的总体差额为 -0.3836×2000=-767.1233万元,推断的应收账款总体余额为6 992.8767万元,可信赖程度为95%的估计区间为[6 992.8767±4.6853] = [6 988.1914-6 997.7620];
(5)基于谨慎性原则,X注册会计师应最终推断应收账款的总体余额为6 986.3014万元。
注:公式(1)n’=(Ur×S×N/Pa)2
公式(2)n=n’/(1+n’/N)
公式(3)