问题
计算题
(18分）如图，一小车静止在光滑水平地面上，车顶用长L=0.8m的细线悬挂一静止小球，小车质量m3=4.0kg，小球质量m2=0.9kg，一质量为m1=0.1kg的子弹以速度v1=10m/s水平射入球内(作用时间极短，g取10m/s2)，求
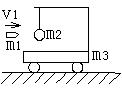
（1）细线上摆的最大角度θ。
（2）小球第一次返回最低点时，小球的速度和小车的速度。
答案
（1）θ=60°
（2）
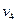=-0.6m/s方向向左；
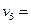0.4m/s方向向右。
（1）子弹与球作用后，子弹与球共同速度v2
子弹与球动量守恒：m1v1=(m1+m2)v2
得v2=1.0m/s 2分
子弹与球摆到最高点时，子弹、球与小车三者达到共同速度v3
子弹、球与小车动量守恒：m1v1=(m1+m2+m3)v3
得v3=0. 2m/s 2分
子弹与球作用后到子弹与球摆到最高点，子弹、球与小车三者机械能守恒
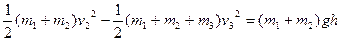
得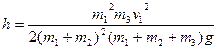
=0.4m 3分
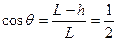得，θ=60°
3分
（2）设小球第一次返回最低点时，小球和小车的速度分别为v4、v5
子弹与球作用后，水平方向动量守恒
(m1+m2)v2=(m1+m2) v4+m3 v5 2分
子弹、球与小车三者机械能守恒
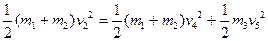2分
得：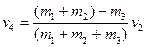
=-0.6m/s方向向左。 2分
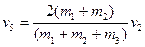=0.4m/s方向向右。 2分