问题
问答题
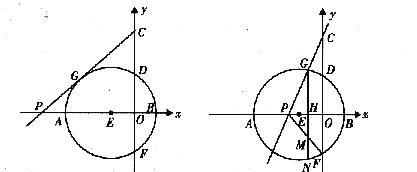
已知抛物线y=-x2*2kx+3k2(k＞0)交x轴于A，B两点，交y轴于点C，以AB为直径的⊙E交y轴于点D，F，如图，且DF：4，点G是劣弧AD上的动点(不与点A，D重合)，直线CG交x轴于点P。
(1)求抛物线解析式；
(2)当直线CG是⊙E的切线时，求tan∠PCO的值；
(3)当直线CG是⊙E的割线时，作GN⊥AB，垂足为点H，交PF于点M，交⊙E于另一点N。
设MN=t，GM=u，求u关于t的函数关系式。
答案
参考答案：
(1)由点A，B是抛物线与x轴的交点，
令-x2-2kx+3k2=0，
解得x1=-3k，x2=k，
则A，B两点的坐标分别为(-3k，0)，(k，0)。
已知抛物线的对称轴方程为x=-k，
则E(-k，0)。
由OE2+OD2=DE2，
∴3k.k=2×2，得k=±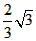 
所以抛物线的方程为y=-x2-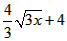
（2）由（1）可知，AO=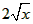
，AB=
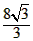，EG=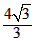
，OC=3k2=4， 连接EG，
∵CG切⊙E于G， ∴∠PGE=∠POC=90°，
∴ Rt△PGE∽ Rt△POC，
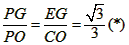
∴ ∵∠PGA=∠PBG，∠GPA=∠BPG，
∴△PGA∽△PBG，
∴PG2=PA.PB=PA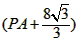 
PO=PA+AO=PA+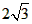
，
代入（*）式整理得PA2+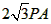
-6=0， 解得PA=3-
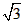（∴PA>0），
∴tan∠PCO=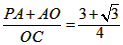
。
（3）∵GN⊥AB，CF⊥AB，
∴GN//CF，
∴△PGH∽△PCO，
∴
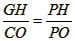
∴ 同理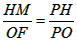 
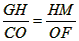
∵CO=4，OF=2，
∴HM=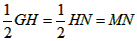
，
∴GM=3MN，即u=3t（0
）。
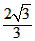