问题
问答题
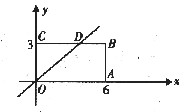
矩形OABC在直角坐标系中的位置，如图，A，C两点的坐标分别为A(6，0)，C(0，3)，直线
与BC边相交于点D。
(1)若抛物线经过D、A两点，试确定此抛物线的表达式；
(2)若以点A为圆心的⊙A与直线OD相切，试求⊙A的半径；
(3)设（1）中抛物线的对称轴与直线OD交于点M，在对称轴上是否存在点Q，以Q、O、M为顶点的三角形与相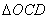
似，若存在，试求出符合条件的Q点的坐标；若不存在，试说明理由.
答案
参考答案：
（1）解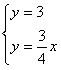 
得D点的坐标为D（4，3） 抛物线
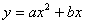经过D（4，3）、A（6，0）， 可得
；
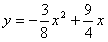（2）∵CD=4，OC=3，OD=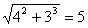
.
sin∠CDO=
，过A作AH⊥OD于H， 则AH=OAsin∠DOA=6×
=
=3.6，
∴当直线OD与⊙A相切时，r=3.6；
（3）①设抛物线的对称轴与x轴交于点Q1，则点Q1符合条件.
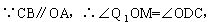
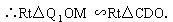
∵对称轴
，∴Q1点的坐标为Q1（3，0）.
②又过O作OD的垂线交抛物线的对称轴于点Q2，则点Q2也符合条件.
∵对称轴平行于y轴，
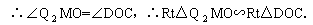
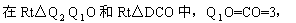
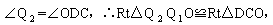
∴CD= Q1Q2=4，∵Q2位于第四象限，
∴Q2（3，-4）. 因此，符合条件的点有两个，分别是Q1（3，0），Q2（3，-4）