问题
问答题
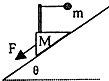
如图所示,在倾角为θ的光滑斜面上,有一质量为M的滑块在平行于斜面的外力F作用下加速下滑,滑块上悬挂小球的细线恰好处于水平方向,小球的质量为m.
试求(1)小球运动的加速度大小;
(2)此时作用在滑块上的外力F的大小.
答案
(1)小球在相互重直的重力和绳的拉力作用下,沿斜面方向以加速度a加速下滑,由牛顿第二定律和力的合成法则得:
F合=ma ①
F合=
②mg sinθ
由①②得:a=g sinθ
(2)小球与滑块相对静止,对整体分析,由牛顿第二定律得
F+(M+m)gsinθ=(M+m)a
解得:F=(M+m)g(
-sinθ).1 sinθ
答:(1)小球运动的加速度大小a=g sinθ
(2)此时作用在滑块上的外力F的大小F=(M+m)g(
-sinθ).1 sinθ
