如图，质量m=25kg的物体在水平外力的作用下在一水平面上运动，物

问题问答题

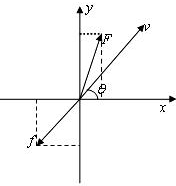
如图，质量m=2

kg的物体在水平外力的作用下在一水平面上运动，物体和水平面间的动摩擦因数μ=0.1，已知物体运动过程中的坐标与时间的关系为x=3.0t（m），y=0.2t²（m），g=10m/s²．根据以上条件求：

（1）t=10s时物体的位置坐标；

（2）t=10s时物体的速度大小；

（3）t=10s时刻水平外力的大小．

答案

（1）、t=10s时，物体在x轴方向运动位移：x=3t=3×10m=30m，

物体在y轴方向运动位移：y=0.2t²=0.2×10²m=20m，

这时物体的位置坐标为（30m，20m）．

（2）、t=10s时，x轴方向的速度：v_x=3m/s，y轴方向的速度为：v_y=at=0.4×10m/s=4m/s，

物体的合速度为：v=

32+42

m/s=5m/s．

（3）、物体的加速度大小为：a=0.4m/s²

物体所受的摩擦力：F_f=μmg=0.1×2

×10N=2

N．方向与合速度方向一致，设与x轴方向的夹角为θ．

则x轴方向的力：F_x=F_fx=F_fcosθ=2

N，

y轴方向的力：F_y-F_fy=ma，解出F_y=F_fsinθ+ma=2

×0.4N=2

×1.2N，

∴水平外力的大小：F=

)2+(2

×1.2)2

N=6N．

答：（1）、t=10s时刻物体的位置坐标是（30m，20m）．

（2）、t=10s时刻物体的速度的大小是5m/s．

（3）、t=10s时刻水平外力的大小是6N．