问题
问答题
计算
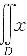 [1+yf(x2+y2)]dxdy,其中D是由y=x3,y=1,x=-1所围成的区域,f(u)为连续函数.
[1+yf(x2+y2)]dxdy,其中D是由y=x3,y=1,x=-1所围成的区域,f(u)为连续函数.
答案
参考答案:令F(x)=
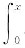 f(t)dt(因为f(u)连续,所以F(x)存在),
f(t)dt(因为f(u)连续,所以F(x)存在),
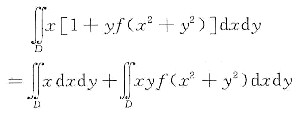
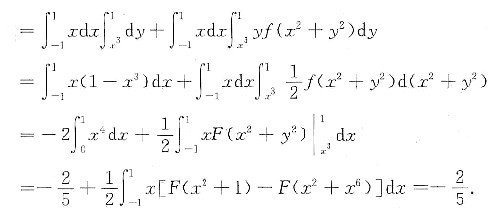
(因为F(x2+1)-F(x2+x6)为偶函数,所以x[F(x2+1)-F(x2+x6)]为奇函数.)
解析:[考点提示] 函数奇偶性的运用.
计算
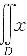 [1+yf(x2+y2)]dxdy,其中D是由y=x3,y=1,x=-1所围成的区域,f(u)为连续函数.
[1+yf(x2+y2)]dxdy,其中D是由y=x3,y=1,x=-1所围成的区域,f(u)为连续函数.
参考答案:令F(x)=
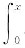 f(t)dt(因为f(u)连续,所以F(x)存在),
f(t)dt(因为f(u)连续,所以F(x)存在),
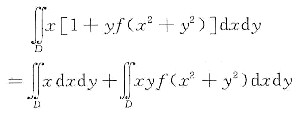
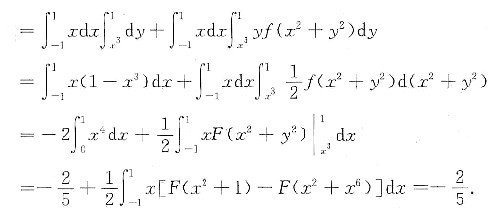
(因为F(x2+1)-F(x2+x6)为偶函数,所以x[F(x2+1)-F(x2+x6)]为奇函数.)
解析:[考点提示] 函数奇偶性的运用.