问题
问答题
已知4阶方阵A=(α1，α2，α3，α4)，α1，α2，α3，α4均为4维列向量，其中α2，α3，α4线性无关，α1=2α2-α3．如果β=α1+α2+α3+α4，求线性方程组Ax=β的通解．
答案
参考答案：令x=(x1，x2，x3，x4)T，则由Ax=(α1，α2，α3，α4)
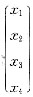=β，得
x1α1+x2α2+x3α3+x4α4=α1+α2+α3+α4，
将α1=2α2-α3代入上式，整理后得
(2x1+x2-3)α2+(-x1+x3)α3+(x4-1)α4=0．
由α2，α3，α4线性无关，知：
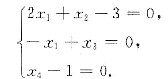
解此方程组得x=
，其中k为任意常数．
解析：[考点提示] 线性方程组求解．