问题
计算题
如图所示，甲车质量为m1=2kg，静止在光滑水平面上，上表面光滑，右端放一个质量为m0=1kg的小物体，可视为质点；乙车质量为m2=4kg，以v0=5m/s的速度向左运动，与甲车碰撞，
碰撞时间极短，且碰后甲车获得v1=4m/s的速度，物体滑到乙车上；若乙车足够长，上表面与物体的动摩擦因数为μ=0.2，求：
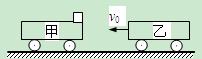
（1）碰撞后乙车的速度v2？
（2）物体在乙车上滑过的痕
迹长度l等于多少？
（3）从碰撞开始经过t=2s时，物体距甲车右端多远？
答案
1）略
2）
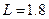m
3）4.64m
解：（1）甲、乙相碰瞬间，小物体速度不变，甲、乙为系统动量守恒，以向左为正向：
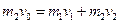
得： m/s，乙碰后向左运动 （4分）
（2）小物块滑到乙车上，与乙车相对静止，令共同速度为u，
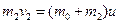
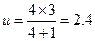m/s，
正号说明u与正方向相同，最终共同向左运动。 （3分）
据能量转化与守恒有：
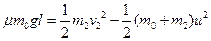
代入数据联解可得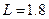：m （3分）
（3）小物块在B上匀加速到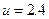
m/s时，令所用时间为t1，有：
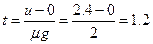s 
（2分）
在此时间内小物块所运动位移：
m
余下时间内小物块所运动位移：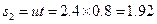
m
物体距甲车右端：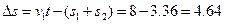
m （4分）