参考答案：

(1)AB证券组合的预期报酬率

＝20%×25%＋12%×75%＝14%　

(2)若两种证券完全正相关，它们的相关系数等于1。

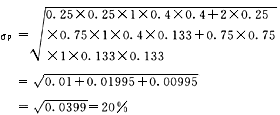
(3)若两种证券完全负相关，它们的相关系数为-1。

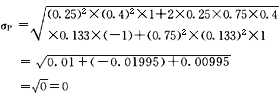
(4)相关系数为0.4时的标准差：

(5)相关系数为-0.4时的标准差：

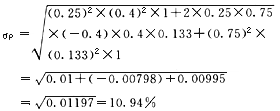
(6)完全投资于A、B证券时的预期报酬率和标准差：　完全投资于A证券的预期报酬率　＝20%×100%＋12%×0＝20%　完全投资于B证券的预期报酬率　

＝20%×0＋12%×100%＝12%　

完全投资于A证券的标准差

完全投资于B证券的标准差

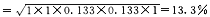
(7)简要说明：

①由计算可知，证券组合的风险(标准差)随相关系数的减小而减小；

②当两种证券完全正相关时，不能抵消任何风险，这时组合的标准差为20%；

③当两种证券完全负相关时，能充分地抵消风险，这时组合的标准差为0；

④当相关系数介于＋1和－1之间时，可以部分地抵消一些风险，如，当相关系数为-0.4时，组合的标准差为10.94%，低于完全正相关时的20%，而且此时证券组合的预期报酬率始终保持14%；这说明，投资者在保持平均报酬率的情况下，可以通过将不完全正相关的资产组合在一起来减少风险。

⑤完全投资于A时的预期报酬率和标准差的坐标点称为最高预期报酬率组合点；完全投资于B时的标准差和预期报酬率的坐标点称为最小方差组合点，有效集是它们之间的那条曲线。