(18分)
题24图中A、B之间为一峡谷,相距2d,C为固定在悬崖上的一根横梁,一箩筐D通过两根轻绳挂在横梁上,当箩筐静止时,它正好处在峡谷AB的正中央,且和峡谷两边的平地差不多在同一水平面上.已知筐的质量为M,每根绳的长度都是l,筐的大小和d相比可忽略不计.现有一人位于峡谷的一边A处,他想到达峡谷的对岸B处,在他身边有很多质量差不多都是m的石块,于是他便不断把石块抛入箩筐,使箩筐动起来,当筐摆恰好到A处时(轻绳与竖直方向夹角未超过10º),他就跨入筐中,当筐摆到B处时,再跨出筐到达B处.如果此人每次只向筐中扔一个石块,当石块击中筐时,筐恰好都位于峡谷的正中央,石块击中筐后随即落在筐内并和筐一起运动,石块击筐的时刻,其速度的大小为v0,方向都是水平的,不计空气阻力,重力加速度为g,试求:
(1)此人从A处进入箩筐到摆动至B处经过的时间.
(2)要使筐摆到A处,此人至少需向箩筐中扔的石块数.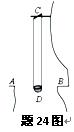
(1)
(2)
(1)箩筐做简谐运动周期
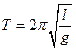 (3分)
(3分)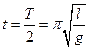 (2分)
(2分)
(2)设第一个石块扔入箩筐后,筐开始运动的速度为 ,由动量守恒定律有
,由动量守恒定律有
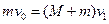 解得:
解得: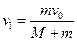 (2分)
(2分)
当第二个石块刚要进箩筐时,箩筐恰好刚回到峡谷中央,速度的大小为 ,方向与石块速度
,方向与石块速度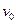 的方向相同,设石块进入筐后,筐的速度为
的方向相同,设石块进入筐后,筐的速度为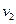 ,由动量守恒定律有
,由动量守恒定律有
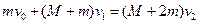 ,由②③两式,得
,由②③两式,得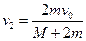 (2分)
(2分)
当第n个石块进入筐时,筐的速度为 (3分)
(3分)
若箩筐具有速度 后,恰好能摆到峡谷的A处,此时,筐上升的高度为h,则由能量关系
后,恰好能摆到峡谷的A处,此时,筐上升的高度为h,则由能量关系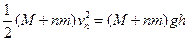 (3分) 而:
(3分) 而: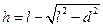 (2分)
(2分)
解得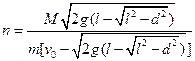 (3分)
(3分)
