问题
单项选择题
下列论断正确的是
(A) 设f(x)在点x=a可导，则|f(x)|在点x=a必可导。
(B) 设f(x)在点a的某邻域U(a,δ)内有定义，且
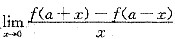存在，则f’(a)必存在.
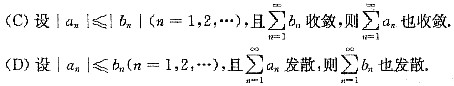
答案
参考答案：D
解析：
[分析]： 由f(x)=x在x=0可导，而|f(x)|=|x|在x=0不可导知，(A)不对．
由f(x)=|x|可说明(B)不对．(f’(0)不存在．)
由[*]发散，这说明(C)不对.
因[*]发散，由|an|≤bn(n=1，2，…)，知bn≥0．依据正项级数比较判别法，知[*]发散，即(D)正确．