问题
多项选择题
设二次型f(x1，x2，x3)=XTAX在正交变换X=PY下的标准形为
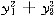，且P的第三列为
．
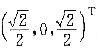(Ⅰ) 求A；
(Ⅱ) 证明A+E为正定矩阵．
答案
参考答案：因为二次型f(xA，xB，xC)=XTAX在正交变换X=PY下的标准形为[*]，所以A的特征值为λA=λB=A，λC=0.P的第三列为[*]，所以λC=0对应的线性无关的特征向量为[*]．因为A为实对称矩阵，所以A的不同特征值对应的特征向量正交，令λA=λB=A对应的特征向量为[*]．
由xA+xC=0的λA=λB=A对应的线性无关的特征向量为[*]
[*]
(Ⅱ) 因为[*]是实对称阵，且A的特征值为λA=λB=A，λC=0,所以A+E的特征值为λA=λB一B，λC=A，因为其特征值都大于零，所以A+E为正定矩阵．
解析：
[分析]： 利用实对称阵的性质导出A；由实对称阵的特征值全大于零证明A+E正定．