问题
问答题
已知三元二次型xTAx的平方项系数均为0,设a=(1,2,-1)T且满足Aa=2a.
(Ⅰ) 求该二次型表达式;
(Ⅱ) 求正交变换X=Qy化二次型为标准形,并写出所用坐标变换;
(Ⅲ) 若A+kE正定,求k的取值.
答案
参考答案:[解] (Ⅰ)据已知条件,有
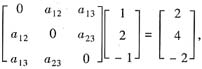

(Ⅱ)由

得矩阵A的特征值为2,2,-4.

得λ=2的特征向量α1=(1,1,0)T,α2=(1,0,1)T;
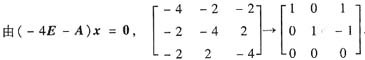
得λ=-4的特征向量α3=(-1,1,1)T.
将α1,α2正交化.令β1=α1,则
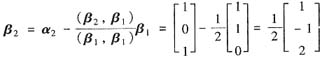
再对β1,β2,α3单位化,有
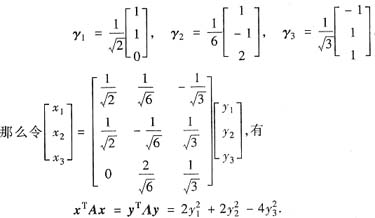
(Ⅲ)因为A+kE的特征值为k+2,K+2,K-4,所以当K>4时,矩阵A+kE正定.
