问题
填空题
设y=y(x)是由方程y2+xy+x2-x=0确定的满足y(1)=-1的连续函数,则
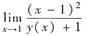 =______.
=______.
答案
参考答案:
解析: 由隐函数存在定理知,由方程y2+xy+x2-x=0确定的满足y(1)=-1的连续函数在x=1邻域必有连续的导数,将方程对x求导得
2yy’+y+xy’+2x-1=0,
解出

[分析二] 由隐函数存在定理知,由方程y2+xy+x2-x=0确定的满足y(1)=-1的隐函数二次连续可导,且
2yy’+xy’+y+2x-1=0, (*)
在(*)式中令x=1,y(1)=-1可得y’(1)=0.将(*)式再对x求导一次,得
2yy’’+2y’2+y’+xy’’+y’+2=0, (**)在(**)式中令x=1,y(1)=-1,y’(1)=0可得
-y’’(1)+2=0
 y’’(1)=2.
y’’(1)=2.
利用洛必达法则和y(1)=-1,y’(1)=0,y’’(1)=2可得
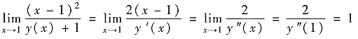
[分析三] 如同[分析二]求出y’(1)=0,y’’(2)=2后,用泰勒公式得