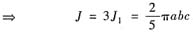问题
问答题
设曲面积分
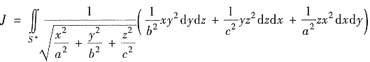
其中S+为上半椭球面：
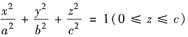的上侧．
(Ⅰ) 求证：
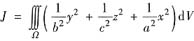，其中Ω是上半椭球体：
；
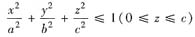(Ⅱ) 求曲面积分J．
答案
参考答案：[分析与求解] (Ⅰ)由题设S+的方程，J可简化成
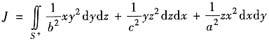
要将曲面积分J化为三重积分，可用高斯公式．由于S+不是封闭曲面，故要添加辅助面
取法向量n向下，S+与S1+所围的区域记为力，它的边界取外侧，于是在Ω上用高斯公式得
其中S1+上的曲面积分为零，因为S1+与yz平面及zx平面均垂直，又在S1+上z=0．
(Ⅱ)求曲面积分J转化为求题(Ⅰ)中的三重积分．怎样计算这个三重积分：
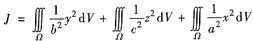
因为Ω是半椭球体，不宜选用球坐标变换与柱坐标变换．我们用先二(先对x，y积分)后一(后对z积分)的积分顺序求
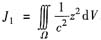
由于z∈[0，c]，与z轴垂直的平面截Ω得区域D(z)为
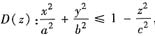
又这个椭圆的两个半轴分别为
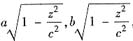面积是
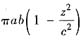，于是
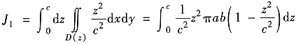
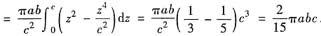
可以用同样方法计算
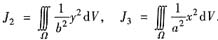
但是，由坐标的轮换对称性，有J1=J2=J3．
