问题
问答题
河宽d=100m,水流速度υ1=3m/s,船在静水中的速度是4m/s,求:
(1)欲使船渡河时间最短,船应怎样渡河?最短时间是多少?船经过的位移是多大?
(2)欲使船航行距离最短,船应怎样渡河?渡河时间多长?
答案
设船与岸成θ角向对岸行驶,如图所示,则当船行到对岸时,s2=d sinθ
t=
=s2 v2 d v2sinθ
当sinθ=1时,t最小,即船应沿垂直与河岸的方向渡河.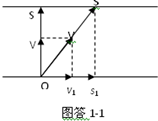
tmin=
=d v2
s=25s;100 4
船经过的位移大小:s=vct;
vc=
=5m/s;
+v 21 v 22
解得:s=5×25=125m;
(2)欲使船航行距离最短,需使船的实际位移(合位移)与河岸垂直,设此时船的开行速度υ2与岸成ϕ角,如图1-2所示.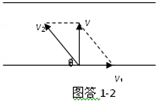
则cosϕ=
=υ1 υ2
,3 4
υ=
=υ22-υ12
m/s=42-32
m/s,7
t=
=d υ
s=100 7
s100 7 7
答:(1)欲使船渡河时间最短,船应垂直河岸渡河,最短时间是25s,船经过的位移是125m;
(2)欲使船航行距离最短,船的合速度垂直河岸渡河,渡河时间
s.100 7 7