参考答案：A

解析： 函数依赖集F成为最小函数依赖集(或最小覆盖)需要满足的条件有：①F中的任何一个函数依赖的右部仅含有一个属性；②F中不存在这样一个函数依赖X→A，使得F与F={X→A}等价；③F中不存在这样一个函数依赖X→A，X有真子集Z使F-{X→A)∪{Z→A)与F等价。
首先将函数依赖集F中左边相同的函数依赖合并，得到{H→IJ，J→K，IJK→L，L→HK}；因为在F中有J→K、IJK→L，K是冗余属性，所以可以合并成IJ→L，即得到新的函数依赖集{H→IJ，J→K，IJ→L，L→HK)，并由此可判知，(1)空缺处选项A是错误的。
接着对所得新的函数依赖集进行化简，进一步得到{H→I，H→J，J→K，IJ→L，L→H，L→K}；由于存在L→H、H→J、J→K，因此可推导出L→K。可见在化简后的函数依赖集中L→K是冗余，可以删除，最后得到(1)空缺处选项B的最小函数依赖集，即为{H→I，H→J，J→K，IJ→L，L→H}。
(1)空缺处选项C中的L→H被去掉了，导致无法从选项C的函数依赖集中根据Armstrong公理系统导出L→H，因此选项C不是正确的答案；同理，由于选项D中的H→J被去掉了，因此该选项也不是正确的答案。
在最小函数依赖集{H→I，H→J，J→K，IJ→L，L→H}中，所有函数依赖的左边属性的并集为{HIJL}。由于有L→H、H→I、H→J，因此可选候选关键字为{L}；同理，由H→I、H→J、IJ→L推导出可选候选关键字为{H}；由IJ→L、J→K、L→H推导出可选候选关键字为{IJ}。可见，关系模式R的候选关键字有3个，分别为{L}、{H}和{IJ}，非主属性为{K}。
第2范式(2NF)定义：若关系模式R∈1NF，且每一个非主属性完全依赖于码，则关系模式R∈2NF。对于本试题，由于有J→K成立，非主属性K是对选候选关键字{IJ}的部分依赖，它不是完全依赖于码，因此关系模式R不属于第2范式(2NF)，而是第1范式(1NF)。
考点链接7.3.1：候选码选择算法
候选码选择算法：对于给定的关系模式R＜U，F＞，其中U为属性集合，F为函数依赖集。
①依照函数依赖集F将R中的所有属性分为L类、R类、LR类和N类属性，令X为L、N类属性的集合，Y为LR类属性集合；
②若

，则X为R的唯一候选码，算法结束：否则，转③；
③逐一取Y中的单一属性A，若

，则XA为候选码，令Y=Y-{A}，转④；
④依次取y中的任意2个、3个……属性与XZ组成属性组，若XZ不包含己求得的候选码，关于F的闭包

，若

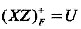，则XZ为候选码。直到取完Y中的所有属性为止，算法结束。
例如，本题在函数依赖集F中无L类和N类属性，所有属性都是LR类属性，因此，X=φ，Y={H，I，J，K，L)。①分别取Y中的单一属性求闭包。

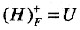，H是候选码；

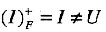，I不是候选码；

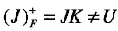，J不是候选码；

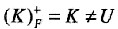，K不是候选码；

，L是候选码。此时Y去掉H和L，Y={I，J，K)。
②取Y中的两个属性求闭包。

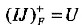，IJ是候选码；

，IK不是候选码；

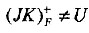，JK不是候选码。因此本题的候选码为：H、L和IJ。