问题
计算题
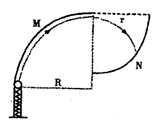
如图是为了检验某种防护罩承受冲击力的装置。M是半径为R=1.0m的固定于竖直平面内的1/4光滑圆弧轨道，轨道上端切线水平，N为待检验的固定曲面，该曲面在竖直面内的截面为半径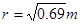
的1/4圆弧，圆弧下端切线水平且圆心恰好位于M轨道的上端点，M的下端相切处放置竖直向上的弹簧枪，可发射速度不同的质量m=0.01kg的小钢珠。假设某次发射的钢珠沿轨道恰好能经过M的上端点，水平飞出后落到曲面N的某一点上，取g=10m/s2。求：
（1）发射该钢球前，弹簧的弹性势能EP多大？
（2）钢珠从M圆弧轨道最高点飞出至落到圆弧N上所用的时间是多少？（结果保留两位有效数字）
答案
（1）0.15J（2）0.24s
（1）设钢球的轨道M最高点的速度为v，在M的最低端速度为v0，则在最高点，
由题意得
①（1分）
从最低点到最高点，由机械能守恒定律得：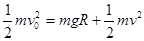
②（1分）
由①②得：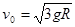
③ （1分）
设弹簧的弹性势能为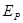
，由机械能守恒定律得：
=0.15J ④ （2分）
（2）钢珠从最高点飞出后，做平抛运动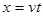
⑤ （1分）
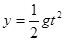⑥ （1分）
由几何关系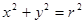
⑦ （2分）
联立⑤、⑥、⑦得t =0.24s （1分）