问题
计算题
如图所示,光滑水平面上有A、B、C三个物块,质量分别为mA = 2.0kg,mB = 1.0kg,mC = 1.0kg.现用一轻弹簧将A、B两物块连接,并用力缓慢压缩弹簧使A、B两物块靠近,此过程外力做108J的功(弹簧仍处于弹性限度内),然后同时释放A、B,弹簧开始逐渐变长,当弹簧刚好恢复原长时,C恰以4m/s的速度迎面与B发生碰撞并粘连在一起.求:
(1)弹簧刚好恢复原长时(B与C碰撞前)A和B物块速度的大小.
(2)当弹簧第二次被压缩时,弹簧具有的最大弹性势能.
答案
(1)弹簧刚好恢复原长时,A和B物块速度的大小分别为υA、υB.
由动量守恒定律有:0 = mAυA - mBυB
此过程机械能守恒有:Ep = 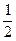 mAυ
mAυ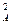 +
+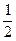 mBυ
mBυ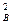
又 Ep=108J
解得:υA=6m/s,υB = 12m/s,A的速度向右,B的速度向左.
(2)C与B碰撞时,C、B组成的系统动量守恒,设碰后B、C粘连时速度为υ′,则有:
mBυB -mCυC = (mB+mC)υ′, 代入数据得υ′ = 4m/s,方向向左.
此后A和B、C组成的系统动量守恒,机械能守恒,当弹簧第二次压缩最短时,弹簧具有的弹性势能最大,设为Ep′,且此时A与B、C三者有相同的速度,设为υ,由动量守恒有:mAυA -(mB+mC)υ′ = (mA+mB+mC)υ,代入数据得υ = 1m/s,υ的方向向右.
由机械能守恒有: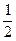 mAυ
mAυ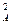 +
+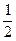 (mB+mC)υ′2 = Ep′+
(mB+mC)υ′2 = Ep′+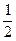 (mA+mB+mC)υ2
(mA+mB+mC)υ2
代入数据得E′p=50J.
