问题
计算题
如图所示两个质量分别为M1、M2的劈A、B，高度相同。放在光滑水平面上，A、B的上表面为光滑曲面，曲面末端与地面相切。有一质量为m的物块（可视为质点）自劈顶端自由下滑。劈顶端到地面距离h=0.06m，劈A与物块的质量比M1/m =5。
求：（I）物块离开A瞬间A和物块的速度各多大？(g=10m/s2)
（II）物块从A上滑下后又冲上B，若要保证物块离开B后不能追上A，则B与物块的质量比M2/m应满足什么条件。
答案
①、设向右为正方向，小球从A滑下的过程
能量守恒：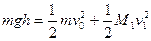 
……………………1分
水平方向动量守恒： mv0－M1v1="0 " ……………………1分
可得： A的速度： v1="0.2m/s " ……………………1分
物块的速度： v0="1.0m/s " ……………………1分
②、物块冲上B又离开的过程：
能量守恒： 
……………………1分
水平方向动量守恒： mv0=M2v2+mv’ ……………………1分
可得：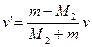
……………………1分
当m<M2时v’<0，当v’的大小不大于v1时m不能再追上A：
即：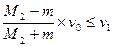
……………………1分
得：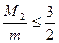
……………………2分