某公司计划从国外引进生产摩托车的生产线，该项目分两期进行：
第一期2011年年初设备投资20000万元，当年投资当年完工投产，年产销量为1万台，销售单价1.2万元/台，单位变动成本0.6万元/台，每年固定付现经营成本为400万元，预计使用寿命为5年，预计能够收回的净残值率为原值的4%。
第二期2013年年初设备投资33000万元，当年投资当年完工投产，年产销量新增到1.9万台，销售单价1.2万元/台，单位变动成本0.58万元/台，年固定付现经营成本新增到760万元，预计使用寿命为5年，净残值率为原值的3%。
假设：
(1)第二期项目投资决策必须在2012年年底决定；
(2)生产摩托车可比公司股票价格的方差为0.09；
(3)该公司适用的所得税税率为25%；
(4)该公司要求的最低投资报酬率为15%(其中无风险报酬率为5%)；
(5)该类设备税法规定的折旧方法为直线法，折旧年限为5年，用直线法计提折旧，净残值率为原值的5%。
要求：
在考虑期权的前提下，计算分析该项目第一期和第二期投资的可行性。
参考答案：
在考虑期权的前提下，分析该项目第一期和第二期投资的可行性：在考虑期权的前提下，可以将第二期投资看作是到期时间为2年的欧式看涨期权。
第二期设备投资的33000万元是期权的执行价格，执行价格的现值为29931万元[33000×(P/F，5%，2)]；第二期设备投资的营业现金流量的现值33534.78万元(28071.79+5462.99，相当于2012年底的数额)，折现到2011年年初为25355.65万元[33534.78×(P/F，15%，2)]，为期权标的资产的目前价格。
根据布莱克-斯科尔斯期权定价模型计算：
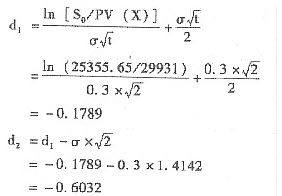
通过N(0.17)=0.5675和N(0.18)=0.5714之间插值来计算N(0.1789)：
N(0.1789)=0.5675+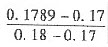
×(0.5714-0.5675)=0.5710
N(-0.1789)=1-N(0.1789)=1-0.5710=0.4290
通过N(0.60)=0.7257和N(0.61)=0.7291之间插值来计算N(0.6032)：
N(0.6032)=0.7257+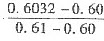
×(0.7291-0.7257)=0.7268
N(-0.6032)=1-N(0.6032)=1-0.7268=0.2732
C0=S0N(d1)-PV(X)N(d2)=25355.65×0.4290-29931×0.2732=10877.57-8177.15=2700.42(万元)。
由于第一期投资考虑期权后的净现值为386.87万元(-2313.55+2700.42)，因此投资第一期和第二期项目均可行。
解析：
本题是按教材的思路来做的，严格来讲这种做法不符合布莱克一斯科尔斯期权定价模型的要求，原因是期权执行价格的现值29931万元[33000×(P/F，5%，2)]不是按连续复利计算的，按布莱克一斯科尔斯期权定价模型的要求，期权执行价格的现值应按连续复利计算，应为29859.63万元(33000×e-5%×2)。