问题
解答题
已知△ABC与△A′B′C′中,AC=A′C′,BC=B′C′,∠BAC=∠B′A′C′=110°
(1)试证明△ABC≌△A′B′C′.
(2)若将条件改为AC=A′C′,BC=B′C′,∠BAC=∠B′A′C′=70°,结论是否成立?为什么?
答案
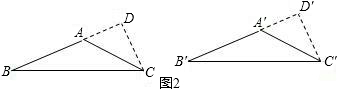
证明:(1)如图1,作CD⊥BA于D,C'D'⊥A'B'.
∵∠BAC=∠B'A'C'=110°,∴∠CAD=∠C'A'D'=70°,
∴△ADC≌△A'D'C'(AAS),∴CD=C'D'.
在Rt△BDC与Rt△B'D'C'中,BC=B'C',CD=C'D'.
∴Rt△BDC≌Rt△B'D'C'(HL),∴∠B=∠B'.
∴在△ABC与△A'B'C'中,∠BAC=∠B′A′C′ ∠B=∠B′ BC=B′C′
∴△ABC≌△A'B'C'(AAS).
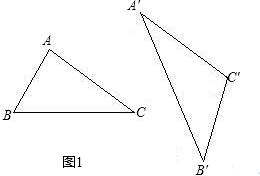
(2)若将条件改为AC=A'C',BC=B'C',∠BAC=∠B'A'C'=70°,结论不一定成立,如图2所示,△ABC与△A'B'C'中AC=A'C',BC=B'C',∠BAC=∠B'A'C'=70°,但△ABC与△A'B'C'显然不全等.