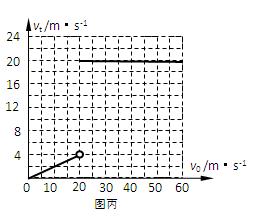
一质量M = 0．8 kg的中空的、粗细均匀的、足够长的绝缘细管，其内表面粗糙、外表面光滑；有一质量为m = 0．2 kg、电荷量为q = 0．1 C的带正电滑块以水平向右的速度进入管内，如图甲所示。细管置于光滑的水平地面上，细管的空间能让滑块顺利地滑进去，示意图如图乙所示。运动过程中滑块的电荷量保持不变。空间中存在垂直纸面向里的水平匀强磁场，磁感应强度为B = 1．0 T。（取水平向右为正方向，g =" 10" m/s2）
（1）滑块以v0 = 10 m/s的初速度进入细管内，则系统最终产生的内能为多少?
（2）滑块最终的稳定速度 vt取决于滑块进入细管时的初速度v0
①请讨论当v0
的取值范围在0至60 m/s的情况下，滑块和细管分别作什么运动，并求出vt 和v0的函数关系？
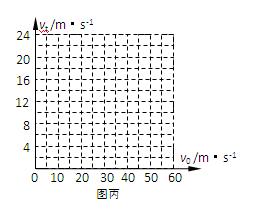
②以滑块的初速度v0横坐标、滑块最终稳定时的速度vt 为纵坐标，在丙图中画出滑块的vt—v0图像（只需作出v0的取值范围在0至60 m/s的图像）。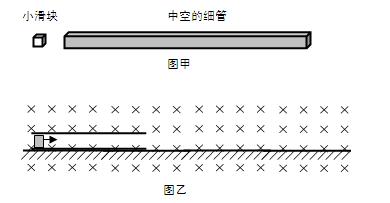
（1）（8分）小球刚进入管内时受到洛仑兹力为：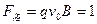
N ① （2分）
依题意小球受洛仑兹力方向向上，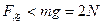
，小球与管的下壁有弹力，摩擦使球减速至最终与细管速度相同时,两者以共同速度v运动 （1分）
由动量守恒定律：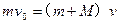
② （2分）
对系统：由能量守恒定律：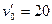
③ （2分）
由②③得：Q =" 8" J （1分）
（2）（10分）如图。
分析：当滑块对管的上下壁均无压力时，滑块进入细管的速度满足：
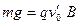④
得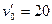：m/s -----------------1分
当滑块初速小于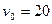
m/s时，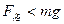
，滑块与管的下壁有弹力，并有摩擦力，使滑块作匀减速直线运动，细管作匀加速直线运动，最终两者共速----------1分
对系统：依动量守恒定律：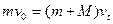
⑤-----------1分
代入数据得：
⑥（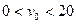
m/s）-----------1分
②当滑块初速20m/s≤v0≤60m/s时，滑块与管的上壁有弹力，摩擦使滑块减速最终速度为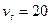
m/s，而细管作匀加速直线运动，加速到V’ ⑧-------1分
当滑块以初速度为v0’进入，若恰好v’=vt=20m/s,则对系统依动量守恒定律有：
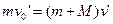
可得：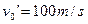
>60m/s
当滑块以v0=60m/s进入时，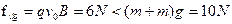
∴细管工不会离开地面。
可见：当滑块以初速度20m/s≤v0≤60m/s进入细管时，细管最终不能加速到20m/s-- 1分
（画图每段2分）
